はじめに
相加平均と相乗平均の関係は、現行過程では数IIの冒頭に登場しますが、あまり深掘りされないまま素通りされてしまっている印象があります。そこで今回から数回にわけて、相加平均と相乗平均をさまざまな角度から考えてみたいと思います。
相加平均と相乗平均の関係とは何か?
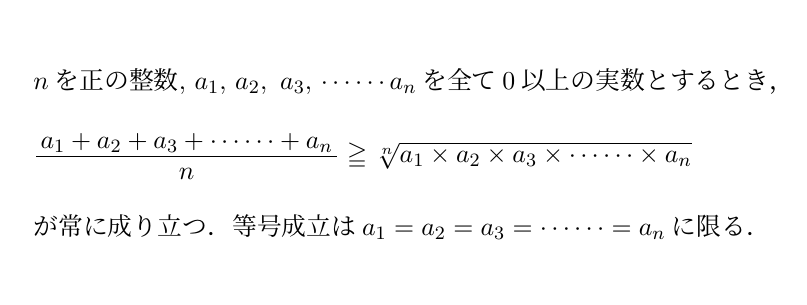
この不等式のうち、左辺を相加平均(算術平均、arithmetic mean)、右辺を相乗平均(幾何平均、geometric mean)といいます。

相加平均と相乗平均の関係は、分母を払って変形した形もよく使います。
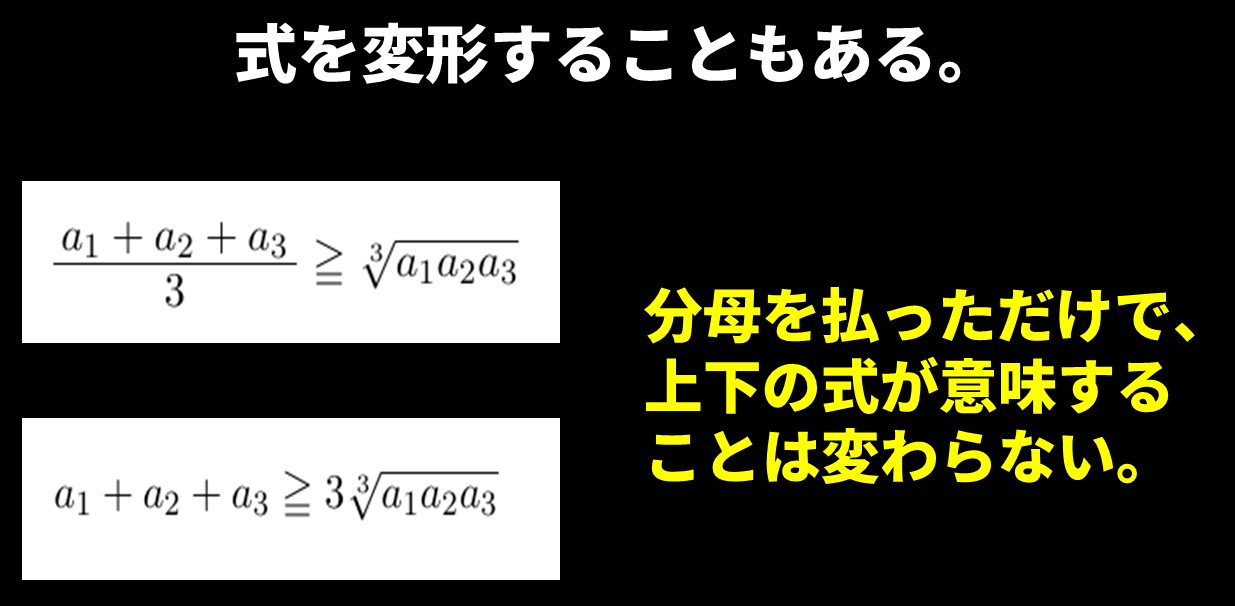
また、n個の数の中に0が1つでも含まれている場合、右辺の相乗平均が0になるので不等式が成り立つことは自明です。したがって、相加平均と相乗平均の関係はn個の0以上の実数について成り立つといえます。

ここから下は、n個の正の数に限定してお話ししていきます。
n=2のとき
(左辺)ー(右辺)を因数分解することで証明できます。
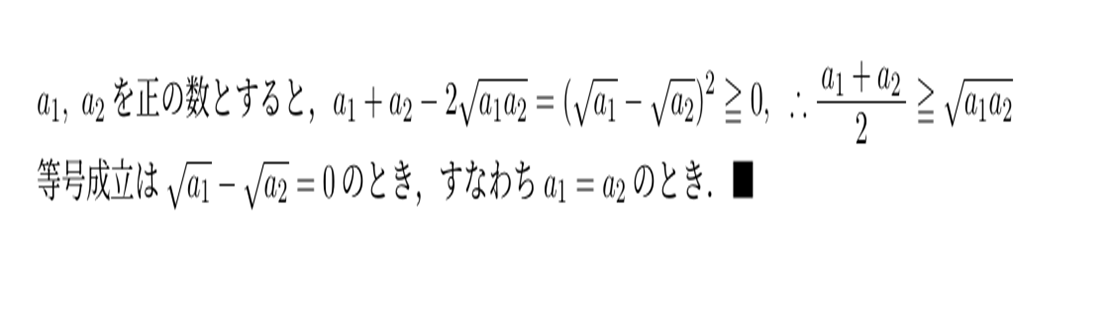
n=3のとき
(左辺)ー(右辺)を因数分解することで証明できます。この因数分解はあまり日の目を見ることが少ないですが、こういうときに役立ちます。また、前に1/2を出す技巧も初見ではなかなか気がつかないでしょう。

n=4のとき
n=2を使うことで示すことができます。実はnが2の累乗(2, 4, 8, 16, 32, ……)のときも同様に示すことができます。

なんとn=4からn=3が示せる!
今回の証明法のメインディッシュに相当する部分ですが、実はn=2→n=4に進んだ後にn=3を示すこともできます。いうなれば「逆向きの帰納法」みたいなものです。よくこんな証明法を思いついたものだと感心します。

この証明法は飛び石から逆戻りというイメージで捉えるとわかりやすいです。
n=2とn=4を使ってn=8を示し、1つ戻ってn=7を示す
この方法はn=2とn=4→n=8→n=7の場合にも応用できます。

さらにn=6を示したい場合は、n=7のときの関係式を使って導き出します。

こうして全ての正の正数nに対して相加平均と相乗平均が示されることになります。なお、nが2の累乗の際に常に成り立つことを言うには数学的帰納法を用いますが、大変煩雑な流れになるので、今回は割愛しました。
おわりに
今回は第一回目ということで、数IAIIBの範囲に限定してお話を進めました。第2回目は関数の凸性など、数IIIの知識も援用しながらさらに深掘りしていきます。