初等幾何, 高校数学, 中学数学, 角の二等分線, 上野丘高校, 舞鶴高校, 医学部受験,

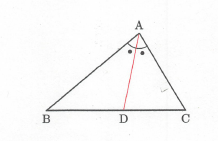
角の二等分線の性質を証明してみよう

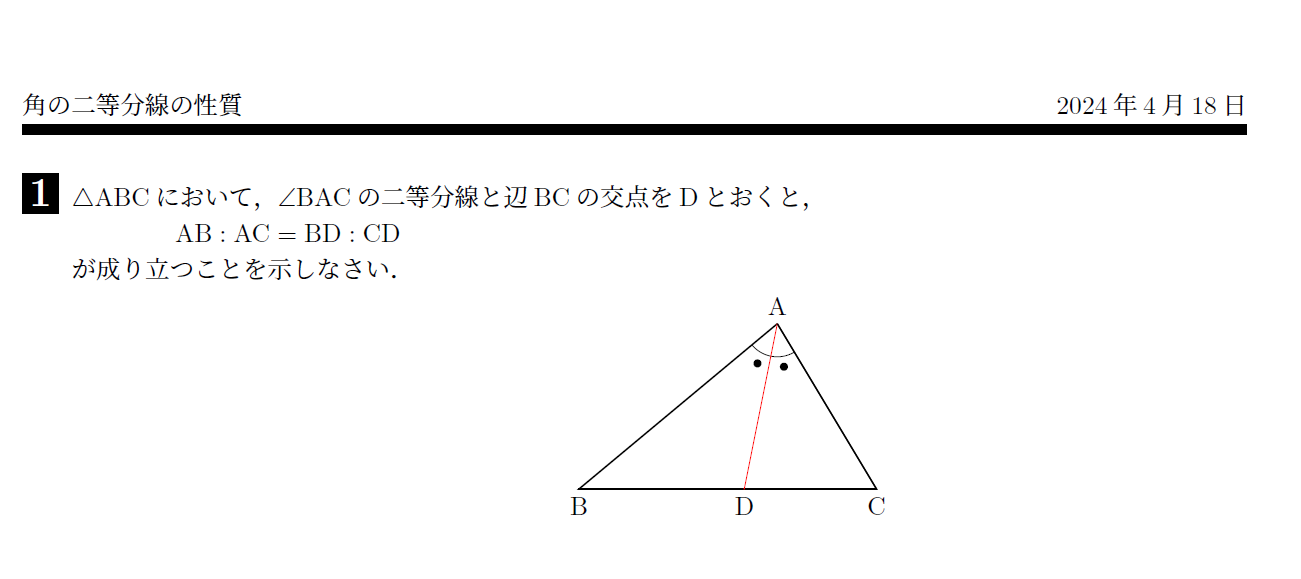
だいぶ前の話ですが、私の生徒が通っている首都圏の中学校の数学課題で、「角の二等分線の性質をできるだけ多くのやり方で証明してきなさい」という課題が出ました。生徒から解法を質問されたので、私も当時いろいろなやり方を考えてみました。このような図形（幾何）の基本的な性質をさまざまな観点で考えてみることは、図形を見る目を養うよい訓練になると思います。

証明その1

高校数学の範囲まで含めると相当な数の証明法が考えられますが、平行線を引いて平行線の線分比の性質に持ち込む方法が基本になります。証明その1では、三角形の外側に平行線を引いてみました。比較的分かりやすいと思います。相似を使わないので、公立中学の3年生でも理解できる（はず）の解法です。

証明その2

同じく三角形の外側に平行線を引いて線分比に持ち込む方法ですが、こちらは中3の終わりの方で習う「相似」を使って解いています。

証明その3

同じく線分比に持ち込む方法ですが、平行線を三角形の中に引くのが特徴です。証明1、証明2と比べて手順が多くなっているので、生徒にはあまり評判がよくありません。

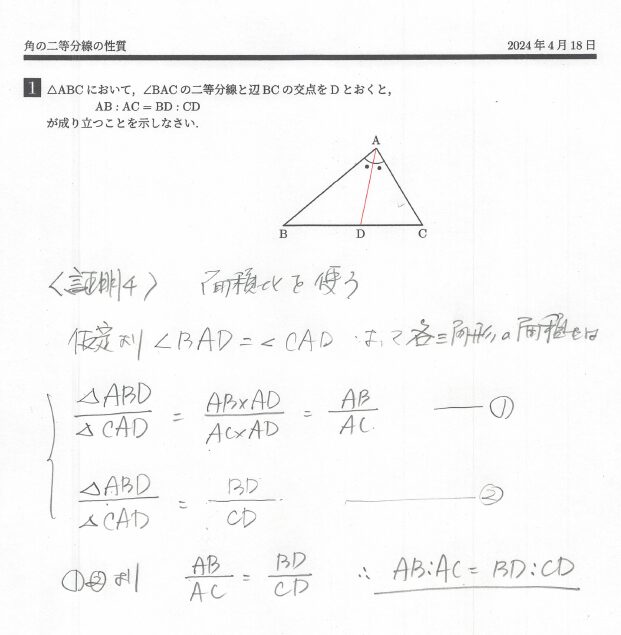
証明その4

平行線を一切使わずに、面積比を利用して解く解法もあります。長さの比を面積比に、面積比を長さの比に、それぞれ置き換えるテクニックは、難関高校受験生なら非常に重要です。一つわかりにくいところがあるとするなら、②については高さが等しい三角形の面積は底辺の長さの比に等しくなることを使えば思いつくでしょうが、問題は①が成り立つ理由です。ヒントとしては、△ABCを直線ADで折り返すとADとACが重なるので、△ABDと△ACDは、辺AB、辺ADを底辺と見たときの高さが等しくなります。したがって△ABDと△ACDは底辺の比に等しくなります。

おまけ

角の二等分線の性質は、さまざまな図形に応用できます。私が個人的に好んでよく使うのは、△ABCの外接円と絡める方法ですが、今回はおまけを2つ紹介するだけにとどめておきます。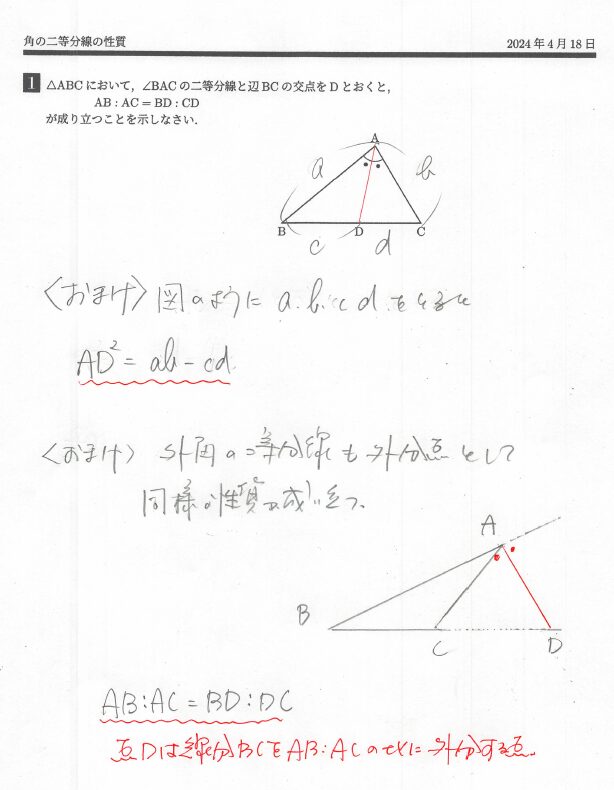

1つ目のおまけは証明するのにちと骨が折れますが、腕に自信がある中学生は挑戦してみてください。円の性質と相似を使うので、中3数学を全て終えていることが前提になります。また、高校生の範囲であれば、ベクトルやsinの面積公式を使うことでもアプローチできます。

2つ目のおまけは、外角の二等分線も同様の性質が成り立つということを示しています。こちらも適当な補助線を引くことにより証明することが可能です。ただ、外分点の扱いに慣れていないと、なかなかピンとは来ないかもしれません。

さらなる初等幾何の学習にオススメの本

初等幾何は高校数学の数Aがよくまとまっているので、高校生用の数学A参考書を使うのが一つの手です。しかし、ありきたりの参考書では満足できない人もいることでしょう。そういう人には、モノグラフの「幾何学～発展的研究法～」がオススメです。オイラー線やナポレオンの定理、フォイエルバッハの9点円など、なんでこんな定理を思いついたのだろうというような不思議な性質がたくさん紹介されています。さらなるマニアには、岩田至康「幾何学大辞典」です。これは唯一無二といってよいほどの大作です。私も補巻以外はすべて買い集めましたが、持っていてもなかなかページを開く機会がなく、宝の持ち腐れになってしまっています.