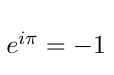
数学はオイラーだらけ
レオンハルト・オイラーは18世紀(1700年代)を代表する偉大な数学者です。彼の残した足跡は中学・高校数学の至るところで確認することができます。ロシア帝国の女帝エカテリーナ2世の庇護を受け、ペテルスブルクに滞在していたこともあり、その際に今日のトポロジーに繋がる「ケーニヒスベルクの橋の問題」を解決するなどしてヨーロッパ中に名声を高めました。
神の存在を証明する公式
また、彼は神の存在についての公開討論会に臨み、神の存在が不可知であると訴える当世一流の啓蒙哲学家ディドロに対し、こう述べました。
$\displaystyle \frac{a+b^n}{n}=x$である。ゆえに神は存在する。
ディドロは自他共に認める知識人の手前、オイラーが投げかけた数式の意味が分からないとは言えず、結局オイラーが勝利しました。この勝利は敬虔なキリスト教徒(正ロシア教会)であるエカテリーナ2世を大いに満足させせたそうです。
オイラーの多面体定理
「オイラーの多面体定理」は中学1年生が立体図形を習うときに出てきます。
$(面の数)+(頂点の数)-(辺の数)=(次元数)-1$
立体図形は3次元なので、右辺は2になります。この関係式が全ての立体について成り立つのです。この定理を用いることで、正多面体が5つしかないことも証明できます。この関係式の覚え方のコツは、「辺はハ行だから引く」です。
高校に入って出てくるオイラーは、「オイラー線」です。三角形の重心と外心と垂心が同一直線上にあるというもので、立体図形についても垂心に相当するものが存在すれば同一直線上にあることが知られています(重心G、外心O、垂心Hとおくと、点Gは線分OHを1:2に内分する)。と。ただ、このオイラー線については授業できちんと扱っている学校は少ないかもしれません。図はWikipedia「オイラー線」からの引用です。

オイラーは晩年になって失明してしまうのですが、論文の執筆ペースは失明の前後で変わらなかったそうです。まさしく「心眼」で数学を見ていたのでしょう。
オイラーの定数γについて
昨日の授業で数IIIの定積分にまつわる不等式を扱いました。そこで出てきたのがこの有名問題です。

青チャートの重要例題ですが、この不等式が意味するものについては、チャートでは詳しく書かれていません。
実は$\displaystyle \lim_{n \to \infty}\left( \displaystyle 1+\frac12 +\frac13+\cdots \cdots +\frac{1}{n}+\cdots -\log n\right)$は一定値に収束することが分かっており、その値$\gamma$は0.5772158…です。この定数$\gamma$をオイラーの定数と呼びます。微積分学の中では$\pi$や$e$の次に重要な定数という人もいるほどです。ただ困ったことに、$\gamma$が一体何者なのかが未だによく分かっていないのです。オイラーの発見から200年以上が経過していますが、有理数なのか無理数なのかさえ不明なままです。
私はこのオイラーの定数について、これまであまり突っ込んで調べたことがなかったので、今週末に何冊か本を読むことにしました。先ほど図書館から借りてきたのが、ジュリアン・ハヴィル『オイラーの定数ガンマ ―γで旅する数学の世界』(共立出版、2009年)です。私の住む田舎町でこの本に興味を持つ読者がいたことも驚きですが、新しい発見があればブログでご紹介する予定です。
1つ目のおまけは証明するのにちと骨が折れますが、腕に自信がある中学生は挑戦してみてください。円の性質と相似を使うので、中3数学を全て終えていることが前提になります。また、高校生の範囲であれば、ベクトルやsinの面積公式を使うことでもアプローチできます。
2つ目のおまけは、外角の二等分線も同様の性質が成り立つということを示しています。こちらも適当な補助線を引くことにより証明することが可能です。ただ、外分点の扱いに慣れていないと、なかなかピンとは来ないかもしれません。
グラフも描けるようになった
LaTeXの描画システムの一つである「TikZ」を使い始めてから数日経ちました。時間はかかるものの、基本的な図形は描けるようになってきたので、今度はグラフの描画に挑戦です。

TikZは全般的に見て非常に優れていますが、ときどきアレ?となることもあります。その一つが直角記号の入力法です。比較的使用頻度が高いコマンドのはずなのに、非常に面倒なやり方で記号を作らないといけないようです。
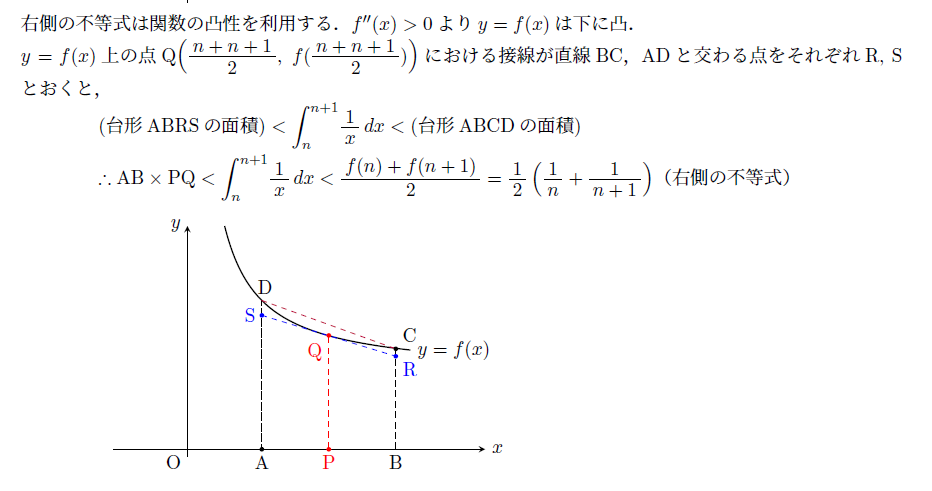
なにはともあれ、グラフもTikZで描けるようになりましたので、今後は数学の問題や解説PDFをどしどし作っていこうと思います。
エラー: コンタクトフォームが見つかりません。
Twitter (X): https://twitter.com/oitatutor
YouTube:https://www.youtube.com/@uptutor




