初等幾何の威力
初等幾何(中学校で習う図形の性質)は大学受験では比較的マイナーな扱いになるので、きちんと修めようとするとたちまち困難に遭遇します。参考書も定番のものがなく、探し出すのに一苦労です(書店だと学習参考書コーナーではなく数学専門書のコーナーに大抵は置いてあります)。その中でも比較的入手しやすいものとして、矢野健太郎監修の『モノグラフ 幾何学~発見的研究法』(科学振興新社)が挙げられます。

私の手元にはこのほか、岩田至康『幾何学大辞典』(1~7巻)や矢野健太郎『ワンポイント 幾何の有名な定理』があります。21世紀の今の時代にこの初等幾何に関する参考書が必要になるのは、数学オリンピックを目指すような人に限られると思いますが、現代的な視点でみると大変興味深い定理もたくさん紹介されており、定理とその証明の流れを暗記しておくとどこかで役に立つこともあります。

しかし今の時代にあって初等幾何の学びを重視する学習塾もあるようで、テキストにもなかなかホネのある問題がたくさん掲載されており、ほとんどの通塾生にしてみれば気の毒なことだろうと痛み入ります。今回はこんな問題を質問されました。
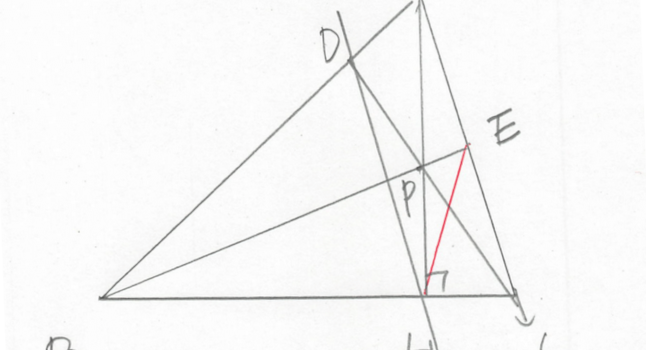
△ABCにおいて,AからBCに下ろした垂線の足をH,Hを通りACに平行な直線とABの交点をD,2直線AH,CDの交点をP,2直線BP,ACの交点をEとおく.このとき,∠AHD=∠AHEを証明せよ.
図に描いてみると次のようになります。
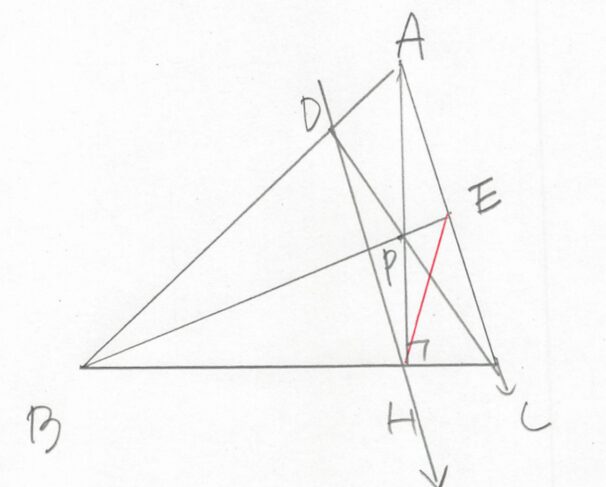
私はこの図を見たとき,「△ABCにおいて辺BCと平行な直線と辺AB,辺ACとの交点をM,Nとおく.線分CMと線分BNとの交点をPとおくと,直線APは辺BCの中点を通る」という初等幾何の性質と証明法をすぐに思い出しました。
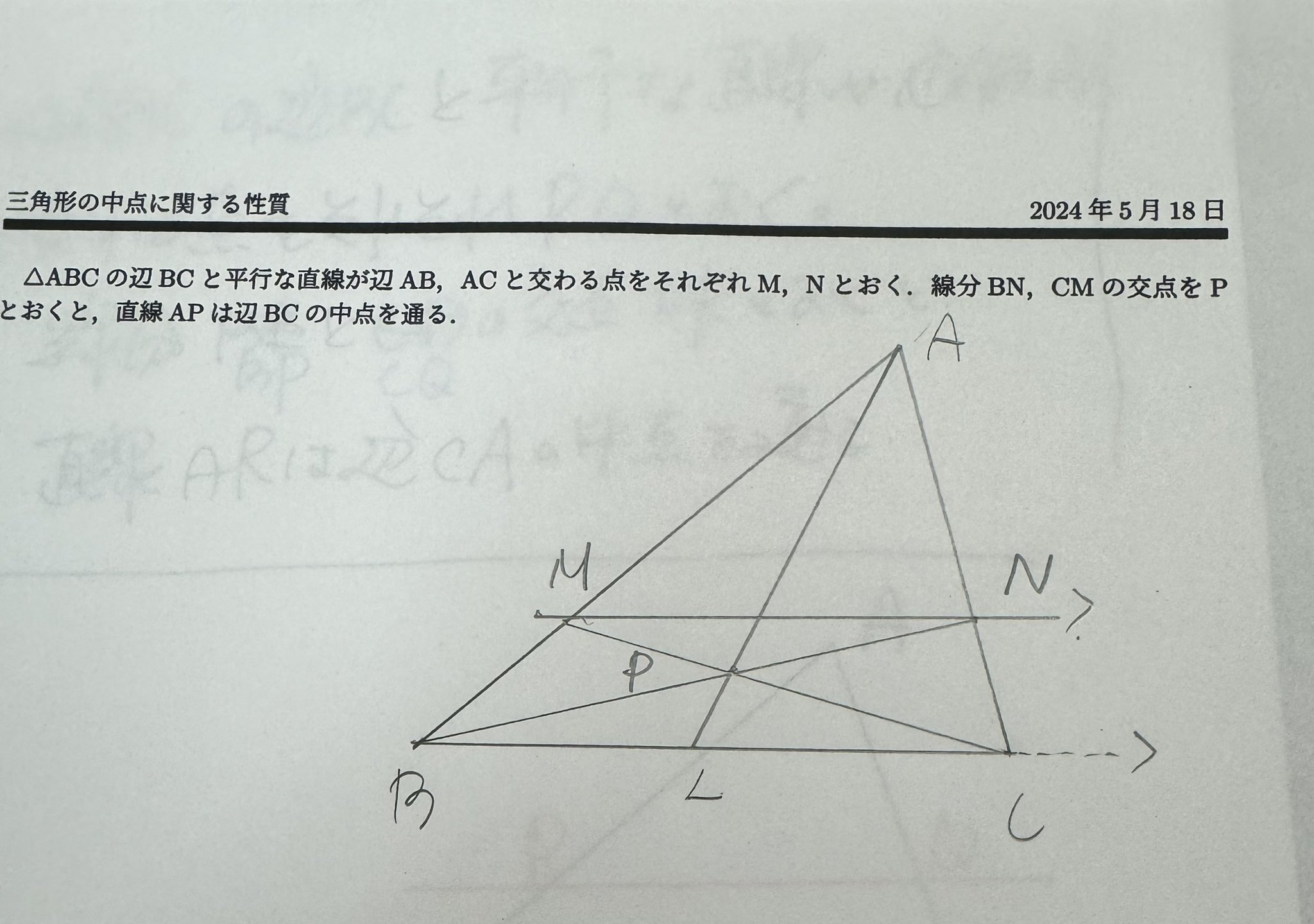
証明法はチェバの定理と平行線の線分比の性質を組み合わせます。直線APと辺BCの交点をLとすると,
MN∥BCより$\displaystyle \frac{\text{AM}}{\text{MB}}=\frac{\text{AN}}{\text{NC}}$
チェバの定理より$\displaystyle \frac{\text{AM}}{\text{MB}}\cdot \frac{\text{BL}}{\text{LC}}\cdot\frac{\text{CN}}{\text{NA}}=1$
この2つの式から$\displaystyle \frac{\text{BL}}{\text{LC}}=1$が導けます。すなわち点Lは辺BCの中点です。
矢野健太郎『ワンポイント 幾何の有名な定理』(pp.60-61)ではこの性質がチェバの定理の応用例として紹介されており、「目盛りのない2つの三角定規を使って辺BCの中点を求めること」ができるとあります。
では冒頭の問題に戻りましょう。上記に示した性質から、辺AC上の点Eは辺BCの中点になることが分かります。このとき,△AHEは∠AHC=90°の直角三角形ですから、点Eは△AHEの外接円の中心です。この円を円Eとすると,EA,EH,ECは円Eの半径なので$\text{EA}=\text{EH}$.
よって△EAHは$\text{EA}=\text{EH}$の二等辺三角形であり,底角が等しいので∠EAH=∠EHA……①
最後に,DH∥ACより錯覚が等しいので∠DHA=∠HAE……②
①②より
∠AHD=∠AHE ■
となります。
塾のテキスト解答がどのように解いていたのか気になりますが、どのルートを辿るにせよ、チェバの定理やメネラウスの定理を扱う単元の問題であることと、三角形の辺の中点に関する性質を知らないと相当な難問ですね。