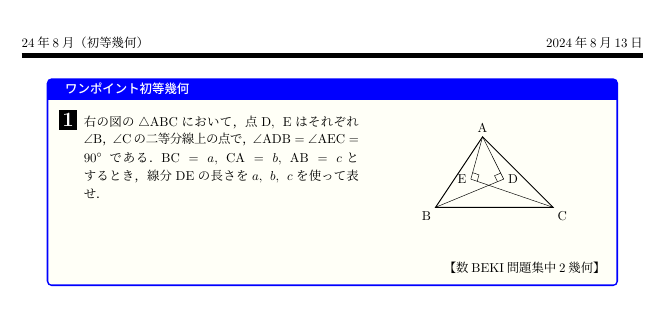
数BEKI問題集
昨日、中高一貫校の中2の生徒から学校で使用している「数BEKI問題集」が難しすぎて分からない、解説してほしいという依頼を受けました。私はこの問題集を今まで使ったことがなかったのですが、問題を一目見ただけで難易度がかなり高く設定されている問題集であることが分かりました。
どこに補助線を引くか?
生徒から質問された問題の中に、なかなか面白い問題があったのでご紹介します。解答例も載せておきますが、出版社の解答を読んでいないので、解答集の解き方とは違う解法の可能性もあります。
初等幾何の問題は適切な場所に補助線を引くことで一気に解決する場合があります。しかし、補助線で埋め尽くされた図形は何を求めたいのか、何をしようとしているのか、見えにくくなる欠点もはらんでいます。この手の問題をたくさん解くことで補助線の「勘どころ」を鍛えていきましょう。問題PDFはこちらにあります。

【解答例】
直線ADと辺BCの交点をP,直線AEと辺BCの交点をそれぞれP, Qとおく.
∠ABD=∠PBD(仮定より),BD=BD(共通),∠ADB=∠BDB=90°(仮定より)であるから,△ABD≡△PBD(二角夾辺相等)
対応する辺の長さは等しいのでAB=PB=c……①
同様にして,∠ACB=∠QCE(仮定より,CE=CE(共通),∠AEC=∠QEC=90°(仮定より)であるから,△AEC≡△QEC(二角夾辺相等)
対応する辺の長さは等しいのでCA=CQ=b……②
①,②とBC=aよりPQ=b+c-a
(BQ+QP=c,CP+PQ=b, BQ+QP+PC=aより)
また,AD=PD, AE=QEより,△APQにおいて中点連結定理からDE=(1/2)PQ = (b+c-a)/2
私は中学生に数学を教える際、中点連結定理のような当たり前に成り立つように見える定理を使う問題ほど難問になりやすいと繰り返し生徒に伝えています。この問題はまさにその意味で「難問」です。
この問題では角の二等分線に下ろした垂線の足がいずれも△ABCの内部にありますが、三角形の形状によっては△の外部にある場合もあります。そのときはDEの長さはどうなるか、研究として考えてみるとさらに知識が広がるでしょう。
自己紹介や授業の詳細につきましては、こちらのページをご覧下さい。
https://uptutor123.com/profile/
★連絡先
メールでの連絡先は
oitatutor@gmail.com
Twitterアカウントは
https://twitter.com/oitatutor
LINE公式アカウントはこちら
YouTubeチャンネルは
https://www.youtube.com/@uptutor
下のお問い合わせフォームもご利用下さい。
エラー: コンタクトフォームが見つかりません。



