Table of Contents

大分県立高校入試（2003年）の問題から

大分県立高校の数学の問題は図形（幾何）の難問が出ることで定評があります。最近は少し傾向が変わり（作問者が変わった？）、テの付け所がないような難問はあまり出題されなくなっている気がしますが、今後また復活する可能性もあるので気が抜けません。

今回から大分県立高校の入試問題から是非とも解いておきたい図形の問題を中心に解説していきます。大分上野丘高校や大分舞鶴高校、中津南高校を目指している中学3年生はぜひ挑戦してみてください。★問題PDFはこちらからダウンロード→大分県2003年幾何

図を大きく描く

図が小さいと大切な条件を見失いやすいので、このような問題の場合は大きく描いてみましょう。

(1) 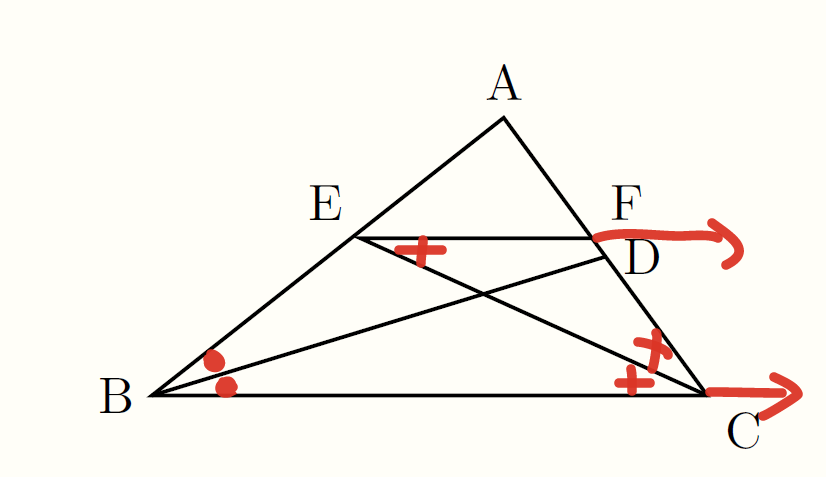EF∥BCより平行線の錯角は等しいので∠FEC=∠ECB……①

条件より∠ECB=∠FEC……②

△FECにおいて，①と②より∠FEC=∠FCEであるから、底角が等しいので，

△FECはFE=FCの二等辺三角形である．■

(2)

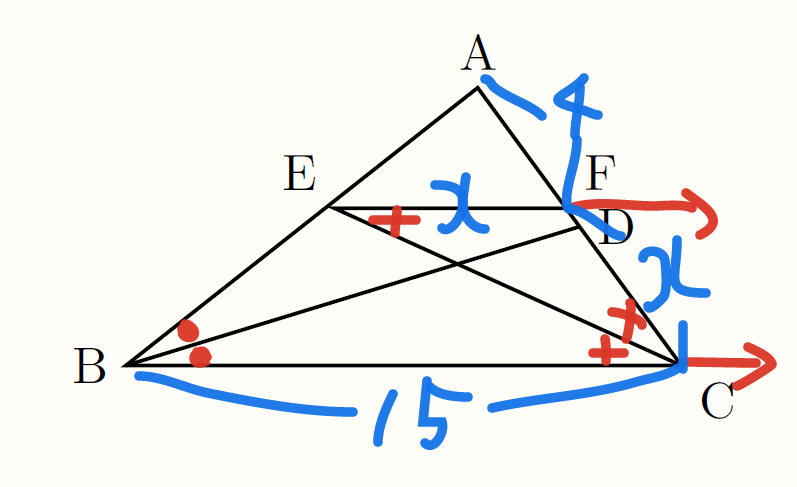
$$\text{EF}=x\, (\text{cm})\text{とおく．}$$

EF∥BCより，△AEF∽△ABC（二角相等）．対応する辺の比は等しいので，AF:FE=AC:CB

$$4:x=(4+x):15,~~(x+10)(x-6)=0,~x=-10,\,6$$

$$x>0\text{より}x=6\, (\text{cm})$$

(3)

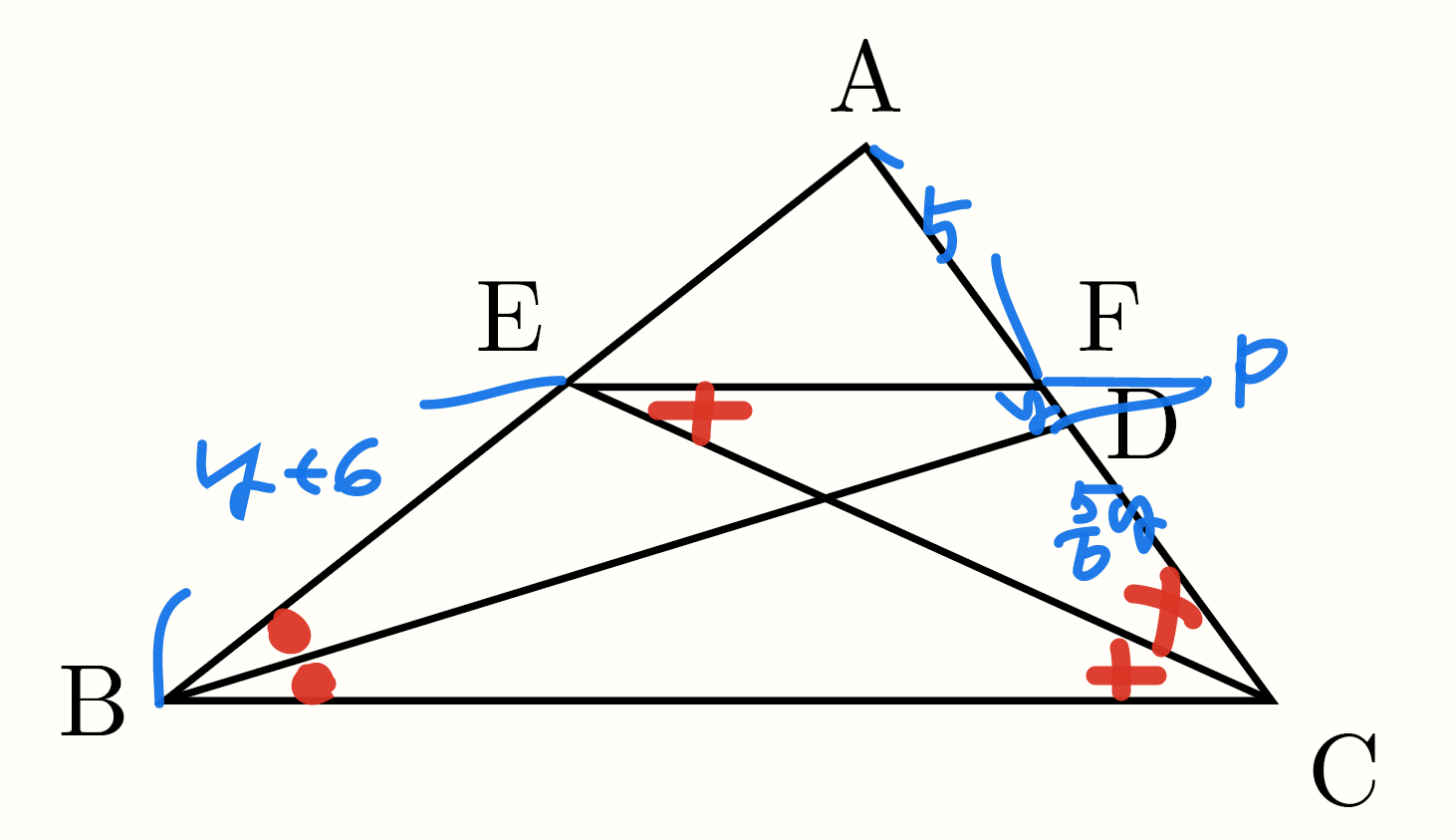
$$\text{直線EFとBDの交点をP}，~\text{FC}=y\,(\text{cm})\text{とおくと，}$$

$$\text{条件より}\text{ED}:\text{DC}=1:5\text{であるから}\displaystyle \text{FD}=\frac{1}{6}y,~\text{DC}=\frac{5}{6}y$$

$$\triangle{\text{EBF}}\text{は}(1)\text{と同様に}\text{EB}=\text{EP}\text{の二等辺三角形であるから，}\text{EB}=\text{EP}=y+6 $$

$$(1)\text{よりFE}=\text{FC}\text{であるから}，\text{EF}=y$$

$$\therefore \text{FP}=6$$

△DFP∽DCP（二角相等）．対応する辺の比は等しいので}

$$\text{DF}:\text{FP}=\text{DC}:\text{CB},~y:6=\frac{5}{6}y:\text{CB},~\therefore \text{CB}=30$$

△AEF∽ABC（二角相等）．対応する辺の比は等しいので

$$\text{AF}:\text{FE}=\text{AC}:\text{CB},~\text{AE}:6=(\text{AE}+6):30,~(y+15)(y-10)=0,~y=-15,~5$$

$$y>0\text{より}y=10$$

さらに△AEF∽ABCより対応する辺の比は等しいので，

$$\text{AE}:\text{EF}=\text{AB}:\text{BC},~\text{AE}:10=(\text{AE}+16):30,~\therefore \text{AE}=8~(\text{cm})$$

次回をお楽しみに。

自己紹介や授業の詳細、お問い合わせ先につきましては、こちらのページをご覧下さい。

https://uptutor123.com/profile/

メールでの連絡先は
oitatutor@gmail.com

LINE公式アカウントはこちら

YouTubeチャンネルは

下のお問い合わせフォームもご利用下さい。

エラー: コンタクトフォームが見つかりません。

大分県立高校入試問題の過去問演習（大分上野丘高校、大分舞鶴高校、中津南高校受験生向け）